Algebra 2 Final Project: "Graphical Creativity: Transforming Functions w/ Desmos

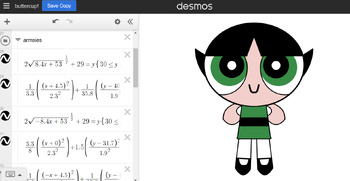
Engage your Algebra 2 students in a creative exploration of functions with this captivating final project. In "Graphical Creativity," students utilize their knowledge of various function types and transformations to design an original image using the Desmos graphing calculator. From rational and exponential functions to sine and cosine curves, students will unleash their creativity while mastering key mathematical concepts.

This project guides students through each step of the process, from brainstorming ideas and preliminary designs to creating equations and restrictions. With clear instructions and deadlines outlined, students will develop essential problem-solving and graphing skills while producing visually stunning artwork.

Encourage collaboration and individuality as students present their unique creations, fostering a classroom environment of creativity and mathematical exploration. Get your students excited about algebra and graphing with "Graphical Creativity: Transforming Functions with Desmos"!